Computers. How do they work? Magic? Bees? Magnets? Who knows. All those components, wires and other bits and bobs, it’s pretty much a mystery that we’ll never really understand. Well, no, actually. Almost nothing (I say almost because, well, you know) could be further from the truth. And it’s worse than that: as part of the ongoing stupidification of society in general, it’s now “cool” to be ignorant of the details even if you work in IT. It gets harder and harder to find good programmers who can write a computer friendly, high performing, memory efficient algorithm because increasingly, none of them have the faintest bloody clue what goes on under the hood. Frankly, for many programmers these days, it might as well be magic, bees and magnets.
The irony of rolling around in such ignorance is that computers are not difficult to understand. At their cores, they are incredibly simple beasts and a doddle to comprehend. I’ll tell you what, I’ll explain it to you and if it goes badly, we can negotiate on how I can send you a compensation slice of one of my truly incredible home made Swiss rolls. It is the most delicious dessert I have ever baked, and I make a mean cake. It contains almost the LD50 of deliciousness, true-facts!
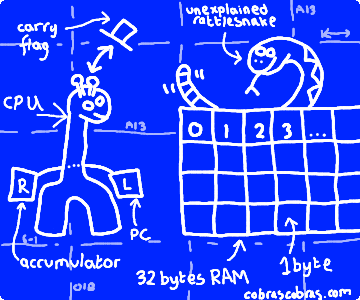
Let’s unpack our example computer who will guide us through this process: the Girafferillo 32. He’s awesomely specified:

If I had had the faintest idea how long this was going to make, I would have drawn it, or grown it, or carved it from granite using hot dog sausages. This represents an extraordinary quantity of work, double sided sticky tape, cardboard and careful cutting when Mrs Cobras was not looking (click for embiggening)
The cardboard boxes are memory locations. Each one of them can store a single number from 0 to 255. If there is nothing in a box, assume it contains zero – I genuinely ran out of steam cutting cardboard and paper. The giraffe itself is the actual computing device. He’s pretty simple. When he’s switched on, he looks in the first box (box zero, top left) and sees what number is in it. That number tells him what to do and how many boxes to move forward to find the next instruction. He keeps track of which box he’s looking in using his “left leg box”, which we will refer to as the LLB. Ok, without further ado, let’s plug this baby in. This could tingle a bit…
Ok, what’s in the first box, Mr Giraffe! Ah yes, code 165. Code 165 means that the next box contains a box number. Look in that box number and copy whatever number it contains into our "right leg box", or RLB, and then add 2 to our LLB so it points at the next instruction. Got that? Ok, so let’s follow the instruction: next box is box 1. It contains the number 28. Let’s look in box 28 – ooooo, the number “2”. Right oh, write “2” on the bit of paper in our RLB and then add 2 to our LLB as ordered.
Lots happened there, so let’s recap our current status. We have followed one instruction and as a result, we have 2 in our RLB and 2 in our LLB. Our LLB tells us which box to look in for our next instruction, which is box 2, so let’s crack on!
Box 2 contains the number 101. Oooooo, different instruction. This one is similar to code 165 but slightly different: the next box contains a box number. Look in that box, and ADD whatever number it contains to what is currently in our RLB and then add 2 to our LLB. Ok, so let’s do that. The next box contains the number 29. Box 29 contains the number 2. Add that to what’s already in our RLB and what do we have? 4. Pop that back into the RLB.
So let us continue. LLB contains 4 so we look inside box 4 for the next instruction. Ah, another new one, 133. 133 follows the same pattern as the other ones: the next box contains a box number. Overwrite whatever is in that box with a copy of what is in our RLB and add 2 to our LLB. Ok, sounds easy. The next box, box 5, contains the number 31. We note down what is in our RLB and pop it into box 31 throwing away what was there when we do it. Awesome. Let’s check out what we’ve ended up with:

Hmmm: looks to me like the Girafferillo has added the contents of box 28 and 29 together and slid the answer into box 31!
And let us see what is next. LLB contains 6 so let’s take a peek at what we’re doing next. Interesting, it contains a zero. Zero means stop, now, do nothing else.
Carry the one… profit!
The Girafferillo 32 has run its first program. The program was this: add the contents of box 28 and 29 together and store the result in box 31. You can run this program again and again with different numbers in boxes 28 and 29 and it will faithfully add them together… or will it? Run the program again, but this time with the numbers 200 and 100 in boxes 28 and 29. Did you get the result 300? If so, you’ve made a mistake. You see, the Girafferillo 32, as I mentioned above, can only store a single number from 0 to 255 in each box – 256 different combinations. When it adds 100 to 200, the RLB will overflow. The result that we will get is the remainder (300 – 256) which is 44, but our giraffe will be wearing the “carry hat” to tell us that this has happened. Let’s check him out in his snazzy hat:
To understand this, we need to take a trip back to school when you were a little girl/boy (delete according to your boobs/moobs status). When you were learning all about numbers, you may recall things like this:
| Thousands | Hundreds | Tens | Units |
|---|---|---|---|
| 103 | 102 | 101 | 100 |
| 0 | 2 | 3 | 4 |
The number 234 is 4 in the units box, 3 in the tens and 2 in the hundreds. Or, (4 x 1) + (3 x 10) + (2 x 100). No box can store anything other than a number from 0 to 9, so if we’re counting up from 0, when we go from 9 to 10, we actually CARRY 1. That means reset our box to zero and add one to the box to the left, meaning we have 0 in the units column and 1 in the tens. If we added 3 to 9, we would end up with 12 – our 9 overflows over to 2 and we carry 1. Got that? Yeah, of course you have! It’s our day to day counting system which is base 10: we have ten digits. Column headers are 10 to the power of 0, 1, 2… etc.
Well, the Girafferillo 32 works the same way except he is using base 256. As a result, he has a units, 256s then 65536s column, etc. When any calculation overflows, I.e., we need to carry one, he puts on the carry hat so that we know.
So at least we know what is going on here. The carry hat means we need to add 1 to the next box, the 256 box, and the remainder, 44, goes in the units.
We reconstitute the whole number like this: 1 x 256 plus 44 x 1 = 300! Awesome. So how do we modify our program to deal with this? Well, firstly, note that I left box 30 un-used, sandwiched uncomfortably between the two numbers we are adding and the result. Well, that is where I plan on storing the number of 256s in the result. As it happens, of course, because we are adding two boxes, the maximum number of 256s will of course be 1: 255 + 255 is 510 which is 254 in the units box and 1 in the 256s box.
Time for a bit of programming. Box 6 currently contains a STOP instruction. Let’s replace it and the following few boxes as follows:
| 6 | 144 |
| 7 | 4 |
| 8 | 230 |
| 9 | 30 |
| 10 | 0 |
Hmm. Interesting. Any detectives want to look at the new boxes and make a rough stab in the dark as to what is happening? Well, there are some clues, so let’s piece together what we can from what we already know. Obviously to the casual observer, this is just a sequence of 5 numbers – but to us, the Girafferillo experts, we can immediately spot some interesting values. Firstly, there is a 30 in the sequence and that’s where we are storing our 256s. There is also a zero at the end, so that’s our STOP instruction. We know that the 144 is definitely an instruction, because it replaces the previous STOP instruction that was there and therefore the chances are that the 230 is an instruction too, and that, given the pattern of INSTRUCTION – BOX NUMBER we’ve seen before, is the one that adds one to our 256 box. So, from guesswork alone, we have established that our new bit of programming does something like this:
- Mystery instruction with 2
- Mystery instruction with 30, probably adding 1
- STOP
Nice! The first mystery instruction, 144, is skip forwards if not wearing the carry hat, and it uses the following box to see how far to skip forwards. Thus, if we are not wearing the carry hat, we add a further 2 to our LLB (the 4 is the total number to add to the LLB if we are not wearing the carry hat) which takes us to the STOP instruction in box 10. If we ARE wearing the carry hat, we proceed to box 8. Instruction 230 means the next box contains a box number, add 1 to whatever is currently inside it.
Bingo. Our add two numbers together program is now complete. No matter what numbers you store in box 28 and 29, the correct result is calculated. The only catch is that we didn’t know whether the Giraffe was wearing his hat when we set out. Usually, to be sure, we’d add an instruction code of “24” before the add instruction. 24 means simply take your hat off.
Gobbledygook, STAT!
It is time to put some proper nerd definitions to our Girafferillo 32. Firstly, those boxes? Each one stores a BYTE. For reasons that we will come to, a byte stores a single integer (no point-something) between 0 and 255. The “32” of our computer’s name corresponds to the amount of memory it has. Thus we have 32 bytes of memory. When you go out and buy a new computer with 4 or 8GB of memory, you are buying one with 4 or 8 BILLION boxes. That is a lot of cardboard, so be thankful for miniaturisation.
Congratulations, you now know more about the low-level operations of computers than most programmers these days, so feel free to take a well deserved trip to the ‘fridge and help yourself to a cool, refreshing beer, or perhaps a glass of wine. Whatever tickles your fancy.
Oh, and one more thing
That’s pretty much it for the first part, and maybe all parts given how damn long it took to make the Girafferillo. However, there is one last thing that you might be amused to know. Our program consisted of the following numbers:
165, 28, 101, 29, 133, 31, 144, 4, 230, 30, 0
Here is our program broken down with the official mnemonics (a text representation of our numbers which we call “assembly language”):
0: 165 28 lda 28 2: 101 29 adc 29 4: 133 31 sta 31 6: 144 4 bcc skip 8: 230 30 inc 30 10: 0 .skip brk
(Five thousand bonus geek points to anyone who already knew that 6502 assembly language was part of the HUD for the Terminator)
I didn’t just make those instruction codes up. Someone else did, back in the mid 70s. These instruction/operation codes, or opcodes, as they’re called, are those of the 8 bit 6502 microprocessor designed in 1975. The 6502 and its variants powered the Apple II, the BBC-B, the Oric, the Atrai 2600 VCS, the Vic 20, the Super Nintendo, the Commodore 64 and numerous other computers that contributed so much to home computing and gaming in the late ’70s and throughout the 1980s. You have just written and understood a program written in 6502 machine code: the lowest level, most complex form of computer programming that is practically possible – manual programming in raw numbers.
If there is any single microprocessor that will give nerds over 35 a good, solid binary erection, it’s the 6502. In fact, I am on the verge of having to rearrange my clock weights just thinking about it. It is difficult to feel any love for any of the other processors of the generation: the Z80 felt like a complete mess (mostly because it was op-code compatible with the 8080) and the 6809 was woefully dated long before the 80s even kicked in. The 6502, though, was a gorgeous, neat, tidy, fast and wonderfully designed piece of kit that struck the perfect balance of complexity and programmer friendliness that was, in my humble opinion, only ever achieved twice. Once with the 6502 that powered, amongst other things, the Apple II, C64 and Atari VCS, and again with the Motorola 68000 that gave life and power to such classics as the Amiga, Atari ST and first generation of Macs. The Girafferillo pays homage to one of the chips that played such an important part in the journey to modern computing.
The 6502 and me
There are some skills that time strips the usefulness from. Skills like rewinding a cassette with a biro or attempting to untangle a barely viewable 15th generation porn video from the VCR before the girlfriend gets home (I succeeded, by the way, but the tape, well, RIP). First the years and then the decades click over and you just know that other than reminiscing about how things were when you were young, these wonderful things will no longer serve a purpose. Now it is just knowledge gathering dust in a dark corner of your brain. You can imagine my surprise, then, when recently I was called upon to attempt to make use of something that I last did in ’91 when I was a lot younger and personal privacy was still something that the everyday person on the street had: programming the 6502 microprocessor in machine code. I had a lot of fun doing it!

I built this, back in ’91. It was supposed to be a Nintendo Gameboy Development system. It worked, after a fashion, but a combination of… well, a lot of things… meant it was never deployed. It uses the 65C102 – a slightly grooved up version of the 6502 with some extra instructions and stuff
But that’s not it for the Girafferillo 32. Next time he’s going to be upgraded to a whopping 256 bytes of memory (needless to say, there will not be a cardboard version) and will come with the ability to display stuff and gather input from the keyboard. All this and more when I release the ‘incredible’ Girafferillo hardware emulator as we bootstrap ourselves through the 80s and our understanding of how computers work.


One Response to Bees: the miracle powering modern computing